Introduction
Cluster Analysis is an important analysis in almost every field of studies. Particularly in business environments, this one analysis plays a critical role in market segmentation and targeting potential customers for higher revenue generation. In simple terms, it is nothing but forming homogeneous groups from a heterogeneous collection of cases/subjects. There are several algorithms available to achieve the goal but applicability of those algorithms differs from situation to situation. In this blog, I am more interested in demonstrating simple, easy to understand clustering technique using readily available tools. In this blog, clustering will be done using Rapidminer. I shall focus on K-means, K-Medoid clustering. I shall also demonstrate how to decide optimum number of clusters based on established indices. Intentionally, the theoretical and mathematical explanations are kept away from this blog. Readers can find detailed explanations in various other websites if they want to understand them in depth.
Once the data is downloaded, it is to be imported into Rapidminer environment. Read CSV operator does the job for you. Drag and drop the operator in the Main Process window. If you can't find the operator, use the search option available in the operators panel. Click on the operator and use Import Configuration Wizard in the parameter panel to load the .csv file (follow the instructions). This file is quite clean and if the instructions are followed properly, no error should be encountered. Afterward, drag and drop the Select Attributes operator in the Main Process window. Connect both these operators (using single clicks on the output and input nodes). The dataset contains channel and regions as attributes and they are nominal in nature (though they are given numbers). Hence, these two attributes should not be included into the clustering processes. Click on the Select Attributes operator and in the parameters panel click on the drop down list. Select the Subset option. Click on the Select Attributes button and transfer 'channel' and 'region' to the right hand side panel. Click on 'Apply' button and mark the check box 'invert selection'. This will ensure that except 'region' and 'channel' all other attributes will be available for the next process. Drag and drop K-Means operator into the Main Process window. By default, the name of the operator will be Clustering. If you want to change the name, press on F2 and rename the operator. Connect this operator with the previous operator. If everything is done properly, the process flow will look like the picture given below.
I am going to run this process with number of clusters as 3 (K=3 in the K-Means operator). The associated XML file is given below.
However, the choice of K is arbitrary in the above process. Many a times, the researcher has some prior knowledge about the possible number of clusters and hence value of K is fixed by means of experiences. However, if the critical information is not available, number of clusters are decided on the basis of certain parameters/criteria. Some of the commonly used criteria are:
1. Silhoutte distance Criteria
2. Akaike Information Criteria (AIC)
3. Bayesian Information Criteria (BIC)
4. Davis Bouldin Index Criteria
5. Cubic Clustering Criteria
6. Between Cluster Criteria
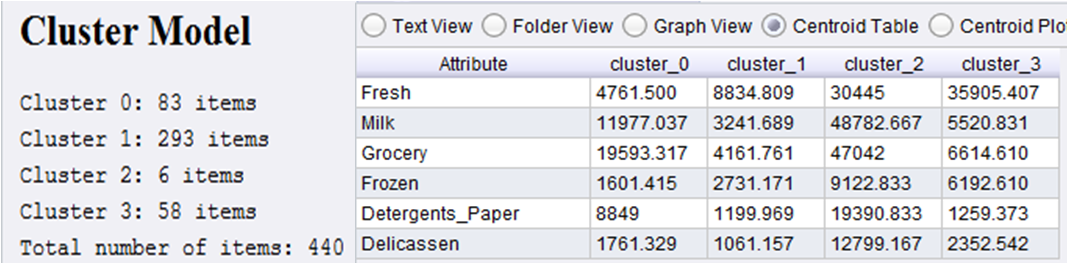
X-Means clustering algorithm is essentially a K-Means clustering where K is allowed to vary from 2 to some maximum value (say 60). For each case BIC is calculated and optimum K is decided on the basis of these BIC values. Details of X-Means clustering can be found here. In the above process, replacing K-Means operator with X-Means operator will serve the purpose. After running the process, X-Means clustering will produce 4 clusters. The cluster model and centroid values are given below.
Clearly, the third cluster (cluster_2) is very important as far sale of items are concerned. These 6 customers are very important customers and they cannot be lost. The 4th cluster customers buy fresh items and they are the second most important customers as far as frozen items are concerned. The 1st cluster customers prefer buying milk, grocery and detergent paper more. The 2nd cluster is probably not that impressive segment although it is the largest cluster as far as number of associated customers are concerned.
Interestingly, when K-Medoid clustering is run, a different result is found. Medoid is the most centrally located data point in a cluster and unlike mean which can take any value in the n-dimensional space, medoid is a physically existing data point and hence restricted compared to simple mean value. K-Medoid is more appropriate when genes are to be segmented or in any situation when the centroid point must also be a physically existing data point. In the following example, I shall demonstrate how to use Optimize Parameters and Set Parameters operators to get optimum K value in case of K-Medoids clustering.
There are 4 ways parameters can be optimized in Rapidminer. These are Grid based, Quadratic based, Evolutionary and Evolutionary (parallel) based. These are very useful when parameter values are to be optimized. These are nested operators and hence, operators are to be optimized must lie within this operator along with one performance measuring operator. Since, K-Medoid clustering is to be used, the same operator must lie within the Optimize Parameters operator. Clsuter distance performance measuring operator is also available in Rapidminer which is required to be connected to the output of K-Medoids operator. The output node of Optimize Parameters operator (node par) is to be connected to Set Paramters operator. Set Parameters operator collects the optimized parameters (OptKMedoids in this case) and supply the same information to another operator (K-Medoids) for doing the clustering. The process flow diagram and parameter setting snapshots are shown in the following pictures.
Running K-Medoids clustering is computationally expensive as compared to X-Means clustering. Hence, more time is required to get the final output. The final outputs are shown below.
The same Optimize Parameters become very handy while dealing with kernel based methods (SVM and kernel based logistic and discriminant analysis). In subsequent blogs I shall demonstrate how to use R functions as well as SAS procedures to do cluster analysis.
K-Means clustering
In the beginning, I shall show how to run simple K-Means clustering and afterward, how to decide optimal number of clusters using automated K-Means clustering (i.e. X-Means clustering) using Rapidminer. Later, I shall use K-Medoid clustering and to decide optimum number of clusters, Davies Bouldin criteria will be used. K-Medoid clustering is considered quite robust in comparison to simple K-Means clustering because means get affected by extreme values (or outliers) whereas, medoids are the most centrally located data point in clusters. I am going to use the wholesale customer dataset to demonstrate the clustering techniques. For this analysis, I am using Rapidminer 5.3.015 version. Rapidminer is one of my favorites because of its simplicity and analysis capabilities. It has operators and each operator performs some dedicated tasks. The entire data analysis process can be captured in the flow diagram and the associated XML codes replicates the same process in another system with just a few clicks! Hence, along with the analysis, the XML codes will also be provided so that readers can play with operators and parameters at their own convenience. So lets begin.Once the data is downloaded, it is to be imported into Rapidminer environment. Read CSV operator does the job for you. Drag and drop the operator in the Main Process window. If you can't find the operator, use the search option available in the operators panel. Click on the operator and use Import Configuration Wizard in the parameter panel to load the .csv file (follow the instructions). This file is quite clean and if the instructions are followed properly, no error should be encountered. Afterward, drag and drop the Select Attributes operator in the Main Process window. Connect both these operators (using single clicks on the output and input nodes). The dataset contains channel and regions as attributes and they are nominal in nature (though they are given numbers). Hence, these two attributes should not be included into the clustering processes. Click on the Select Attributes operator and in the parameters panel click on the drop down list. Select the Subset option. Click on the Select Attributes button and transfer 'channel' and 'region' to the right hand side panel. Click on 'Apply' button and mark the check box 'invert selection'. This will ensure that except 'region' and 'channel' all other attributes will be available for the next process. Drag and drop K-Means operator into the Main Process window. By default, the name of the operator will be Clustering. If you want to change the name, press on F2 and rename the operator. Connect this operator with the previous operator. If everything is done properly, the process flow will look like the picture given below.
I am going to run this process with number of clusters as 3 (K=3 in the K-Means operator). The associated XML file is given below.
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<process version="5.3.015">
<context>
<input/>
<output/>
<macros/>
</context>
<operator activated="true" class="process" compatibility="5.3.015" expanded="true" name="Process">
<process expanded="true">
<operator activated="true" class="read_csv" compatibility="5.3.015" expanded="true" height="60" name="Read CSV" width="90" x="45" y="30">
<parameter key="csv_file" value="C:\Users\Subhasis\Dropbox\Datasets\Wholesale customers data.csv"/>
<parameter key="column_separators" value=","/>
<parameter key="first_row_as_names" value="false"/>
<list key="annotations">
<parameter key="0" value="Name"/>
</list>
<parameter key="encoding" value="windows-1252"/>
<list key="data_set_meta_data_information">
<parameter key="0" value="Channel.true.integer.attribute"/>
<parameter key="1" value="Region.true.integer.attribute"/>
<parameter key="2" value="Fresh.true.integer.attribute"/>
<parameter key="3" value="Milk.true.integer.attribute"/>
<parameter key="4" value="Grocery.true.integer.attribute"/>
<parameter key="5" value="Frozen.true.integer.attribute"/>
<parameter key="6" value="Detergents_Paper.true.integer.attribute"/>
<parameter key="7" value="Delicassen.true.integer.attribute"/>
</list>
</operator>
<operator activated="true" class="select_attributes" compatibility="5.3.015" expanded="true" height="76" name="Select Attributes" width="90" x="179" y="30">
<parameter key="attribute_filter_type" value="subset"/>
<parameter key="attributes" value="|nb.repeat|instr|difficulty|class|attendance|Channel|Region"/>
<parameter key="invert_selection" value="true"/>
</operator>
<operator activated="true" class="k_means" compatibility="5.3.015" expanded="true" height="76" name="K-Means" width="90" x="313" y="30">
<parameter key="k" value="3"/>
</operator>
<connect from_op="Read CSV" from_port="output" to_op="Select Attributes" to_port="example set input"/>
<connect from_op="Select Attributes" from_port="example set output" to_op="K-Means" to_port="example set"/>
<connect from_op="K-Means" from_port="cluster model" to_port="result 1"/>
<connect from_op="K-Means" from_port="clustered set" to_port="result 2"/>
<portSpacing port="source_input 1" spacing="0"/>
<portSpacing port="sink_result 1" spacing="0"/>
<portSpacing port="sink_result 2" spacing="0"/>
<portSpacing port="sink_result 3" spacing="0"/>
</process>
</operator>
</process>
Readers can simply copy-paste the above XML code into the XML tab in Rapidminer to generate the same process flow diagram.However, the choice of K is arbitrary in the above process. Many a times, the researcher has some prior knowledge about the possible number of clusters and hence value of K is fixed by means of experiences. However, if the critical information is not available, number of clusters are decided on the basis of certain parameters/criteria. Some of the commonly used criteria are:
1. Silhoutte distance Criteria
2. Akaike Information Criteria (AIC)
3. Bayesian Information Criteria (BIC)
4. Davis Bouldin Index Criteria
5. Cubic Clustering Criteria
6. Between Cluster Criteria
X-Means clustering algorithm is essentially a K-Means clustering where K is allowed to vary from 2 to some maximum value (say 60). For each case BIC is calculated and optimum K is decided on the basis of these BIC values. Details of X-Means clustering can be found here. In the above process, replacing K-Means operator with X-Means operator will serve the purpose. After running the process, X-Means clustering will produce 4 clusters. The cluster model and centroid values are given below.
Interestingly, when K-Medoid clustering is run, a different result is found. Medoid is the most centrally located data point in a cluster and unlike mean which can take any value in the n-dimensional space, medoid is a physically existing data point and hence restricted compared to simple mean value. K-Medoid is more appropriate when genes are to be segmented or in any situation when the centroid point must also be a physically existing data point. In the following example, I shall demonstrate how to use Optimize Parameters and Set Parameters operators to get optimum K value in case of K-Medoids clustering.
There are 4 ways parameters can be optimized in Rapidminer. These are Grid based, Quadratic based, Evolutionary and Evolutionary (parallel) based. These are very useful when parameter values are to be optimized. These are nested operators and hence, operators are to be optimized must lie within this operator along with one performance measuring operator. Since, K-Medoid clustering is to be used, the same operator must lie within the Optimize Parameters operator. Clsuter distance performance measuring operator is also available in Rapidminer which is required to be connected to the output of K-Medoids operator. The output node of Optimize Parameters operator (node par) is to be connected to Set Paramters operator. Set Parameters operator collects the optimized parameters (OptKMedoids in this case) and supply the same information to another operator (K-Medoids) for doing the clustering. The process flow diagram and parameter setting snapshots are shown in the following pictures.
 |
| Actual K-Medoid Clustering Process |
 |
| Operators within Optimize Parameters operator |
 |
| K values are to be changed from 2 to 10 by 10 steps |
 |
| Set Parameter name map |
 |
| Output of K-Mediods clustering |
The outputs of K-Medoid clustering look sub-optimal in comparison to X-Means clustering in the current context. The high purchasing customers got lost in 2nd cluster and 3rd cluster. However, in other dataset this clustering technique might prove to be superior to X-Means clustering. The XML code for the above mentioned process is given below.
<?xml version="1.0" encoding="UTF-8" standalone="no"?> <process version="5.3.015"> <context> <input/> <output/> <macros/> </context> <operator activated="true" class="process" compatibility="5.3.015" expanded="true" name="Process"> <process expanded="true"> <operator activated="true" class="read_csv" compatibility="5.3.015" expanded="true" height="60" name="Read CSV" width="90" x="45" y="30"> <parameter key="csv_file" value="C:\Users\Subhasis\Dropbox\Datasets\Wholesale customers data.csv"/> <parameter key="column_separators" value=","/> <parameter key="first_row_as_names" value="false"/> <list key="annotations"> <parameter key="0" value="Name"/> </list> <parameter key="encoding" value="windows-1252"/> <list key="data_set_meta_data_information"> <parameter key="0" value="Channel.true.integer.attribute"/> <parameter key="1" value="Region.true.integer.attribute"/> <parameter key="2" value="Fresh.true.integer.attribute"/> <parameter key="3" value="Milk.true.integer.attribute"/> <parameter key="4" value="Grocery.true.integer.attribute"/> <parameter key="5" value="Frozen.true.integer.attribute"/> <parameter key="6" value="Detergents_Paper.true.integer.attribute"/> <parameter key="7" value="Delicassen.true.integer.attribute"/> </list> </operator> <operator activated="true" class="select_attributes" compatibility="5.3.015" expanded="true" height="76" name="Select Attributes" width="90" x="179" y="30"> <parameter key="attribute_filter_type" value="subset"/> <parameter key="attributes" value="|nb.repeat|instr|difficulty|class|attendance|Channel|Region"/> <parameter key="invert_selection" value="true"/> </operator> <operator activated="true" class="multiply" compatibility="5.3.015" expanded="true" height="94" name="Multiply" width="90" x="313" y="30"/> <operator activated="true" class="optimize_parameters_grid" compatibility="5.3.015" expanded="true" height="94" name="Optimize Parameters (Grid)" width="90" x="447" y="30"> <list key="parameters"> <parameter key="OptKMedoids.k" value="[2.0;10;10;linear]"/> </list> <process expanded="true"> <operator activated="true" class="k_medoids" compatibility="5.3.015" expanded="true" height="76" name="OptKMedoids" width="90" x="78" y="39"> <parameter key="k" value="10"/> </operator> <operator activated="true" class="cluster_distance_performance" compatibility="5.3.015" expanded="true" height="94" name="Performance" width="90" x="246" y="30"> <parameter key="main_criterion" value="Davies Bouldin"/> </operator> <connect from_port="input 1" to_op="OptKMedoids" to_port="example set"/> <connect from_op="OptKMedoids" from_port="cluster model" to_op="Performance" to_port="cluster model"/> <connect from_op="OptKMedoids" from_port="clustered set" to_op="Performance" to_port="example set"/> <connect from_op="Performance" from_port="performance" to_port="performance"/> <portSpacing port="source_input 1" spacing="0"/> <portSpacing port="source_input 2" spacing="0"/> <portSpacing port="sink_performance" spacing="0"/> <portSpacing port="sink_result 1" spacing="0"/> </process> </operator> <operator activated="true" class="set_parameters" compatibility="5.3.015" expanded="true" height="76" name="Set Parameters" width="90" x="581" y="30"> <list key="name_map"> <parameter key="OptKMedoids" value="K-Medoids"/> </list> </operator> <operator activated="true" class="k_medoids" compatibility="5.3.015" expanded="true" height="76" name="K-Medoids" width="90" x="447" y="210"/> <connect from_op="Read CSV" from_port="output" to_op="Select Attributes" to_port="example set input"/> <connect from_op="Select Attributes" from_port="example set output" to_op="Multiply" to_port="input"/> <connect from_op="Multiply" from_port="output 1" to_op="Optimize Parameters (Grid)" to_port="input 1"/> <connect from_op="Multiply" from_port="output 2" to_op="K-Medoids" to_port="example set"/> <connect from_op="Optimize Parameters (Grid)" from_port="parameter" to_op="Set Parameters" to_port="parameter set"/> <connect from_op="K-Medoids" from_port="cluster model" to_port="result 1"/> <connect from_op="K-Medoids" from_port="clustered set" to_port="result 2"/> <portSpacing port="source_input 1" spacing="0"/> <portSpacing port="sink_result 1" spacing="0"/> <portSpacing port="sink_result 2" spacing="0"/> <portSpacing port="sink_result 3" spacing="0"/> </process> </operator> </process>
The same Optimize Parameters become very handy while dealing with kernel based methods (SVM and kernel based logistic and discriminant analysis). In subsequent blogs I shall demonstrate how to use R functions as well as SAS procedures to do cluster analysis.
hi guys.
ReplyDeleteis there any one who knows why the DBI (Davies Bouding Index) in rapid miner is negative after a clustering??
i think always, it must be positive.
tnQ
just look at the absolute value http://rapidminernotes.blogspot.dk/2011/04/how-average-within-cluster-distance-is.html
DeleteGood post Machine learning Online Training
ReplyDeleteCool and I have a neat present: Where To Buy Houses For Renovation house remodeling near me
ReplyDelete